X-ray diffraction is a powerful tool for investigating the crystalline structure of materials. When a material is bombarded with X-rays, the waves scatter in all directions. However, when the wavelength of the X-rays is the same as the spacing between atoms in a crystal, the waves will interfere with each other constructively, resulting in a bright spot on an X-ray detector. The position and intensity of this spot can be used to determine the spacing between atoms in the crystal and hence its three-dimensional structure.
X-ray diffraction was first used to study crystals in 1912 by Max von Laue, who showed that it could be used to determine their atomic structures. Since then, it has become one of the most important techniques in structural biology, allowing scientists to determine the structures of proteins, DNA and other biomolecules at atomic resolution. It has also been used to study minerals, metals and other inorganic materials.
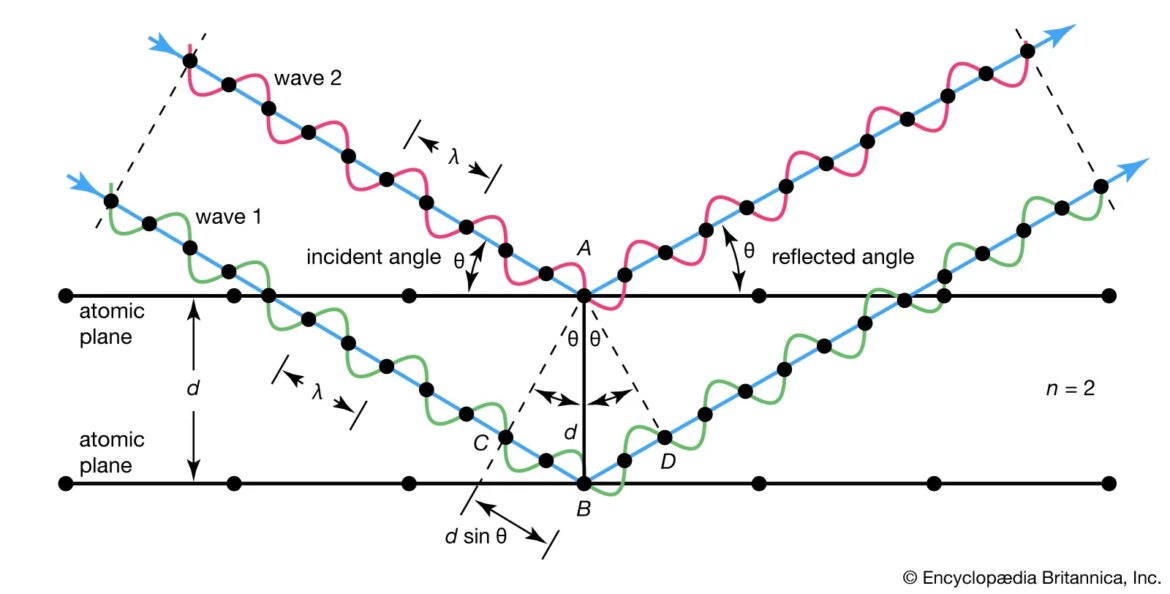
The basic principle behind X-ray diffraction is relatively simple: when a beam of X-rays encounters a crystal, it scatters off of the atoms inside that crystal. The pattern of scattering can be described mathematically using Bragg’s law:
nλ = 2dsinθ
where n is an integer (1, 2, 3…), λ is the wavelength of the incident radiation, d is the spacing between planes of atoms in the crystal (the so-called “lattice constant”), and θ is angle between incoming beam and scattered beam (measured from perfect reflection). This equation says that when conditions are right for constructive interference — that is when nλ equals twice d times sinθ — then we will see a bright spot in our detector. To solve this equation for d we need to know two things: 1) what value or range of values does n take?, and 2) what angles do we expect to see scattering? These two pieces of information define what’s called an “indexing problem”. In general there are many possible solutions to an indexing problem — that is many different values of d that fit our data — but often there are additional constraints that help us narrow down these possibilities (for example if we know something about how big or small our unit cell must be). Once we have determined d for all relevant Miller indices (hkl), we can use these values along with known values for sinθto calculate interatomic distances within our crystal using Pythagoras’ theorem: d(hkl) = √[ h2 + k2 + l2 ]×d(100). This gives us enough information to produce a ball-and‐stick model showing where each atom lies within our unit cell; such models are commonly seen in scientific papers describing new protein or DNA structures solved by x‐ray crystallography.
It should be noted that not all crystals can be studied by x‐ray diffraction; some amorphous materials like glass do not scatter x‐rays evenly enough to produce useful data while others may absorb too much radiation before it ever reaches our detectors. In addition, even some well‐ordered crystals may present difficulties if they are too small or too large; very small crystals (<0.5mm3) tend not produce strong enough scattered beams while very large (>10cm3) ones may suffer from internal stress which distorts their lattices enough to make precise measurements difficult . Nonetheless x‐ray diffraction remains one essential tool for studying condensed matter physics as well as biochemical processes taking place inside cells