A recent study has established a mathematical link between the pattern formation theories of renowned mathematician Alan Turing and the dynamics of sperm tail movement. This seminal research not only enriches our comprehension of natural patterns but also suggests possible applications in medical science and robotics.
Researchers have discovered a connection between the spontaneous motility of sperm tails and Alan Turing’s theories on pattern formation, thereby revealing possible future applications in healthcare and robotics.
Natural patterns such as stripes and spots are believed to originate from chemical interactions. The study reveals that the mathematical principles governing these patterns also control the motion of sperm tails.
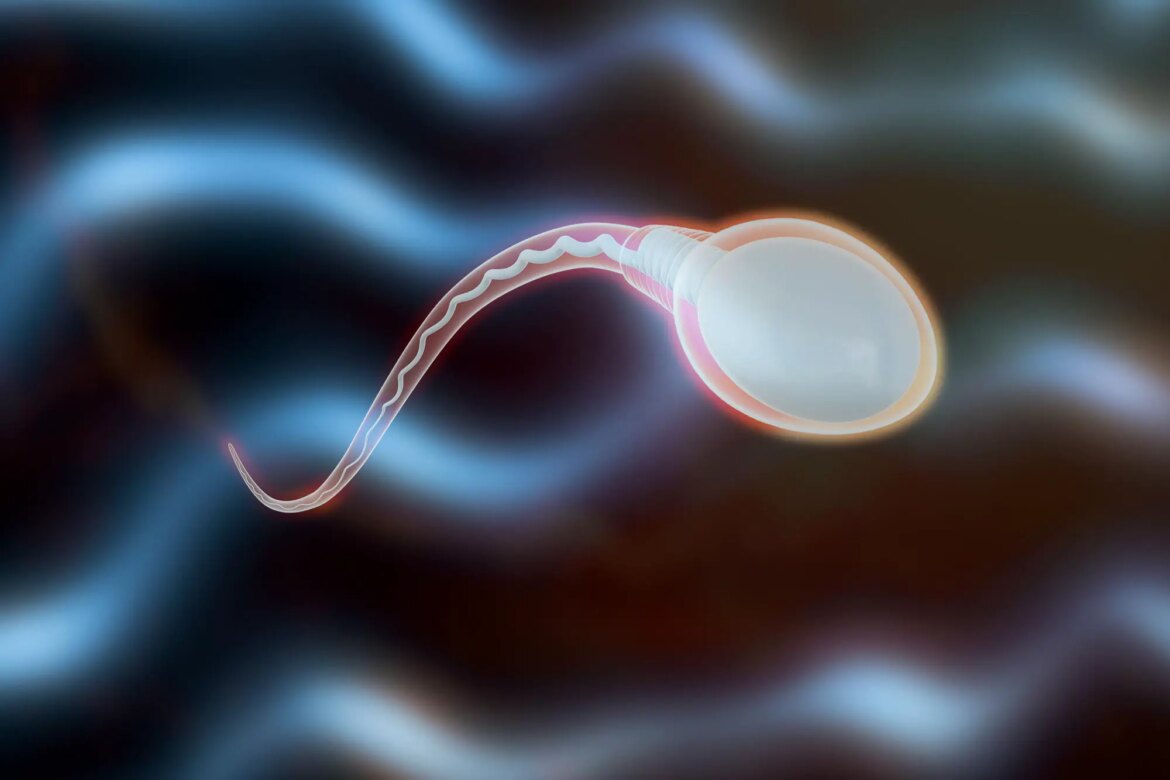
Released today (September 27) in the journal Nature Communications, the study establishes that the movement of flagella, such as those found in sperm tails and cilia, follows the same mathematical framework for pattern formation first formulated by Alan Turing.
Undulations in flagellar structure create spatiotemporal stripe patterns, generating waves that propagate along the tail to propel sperm and microbes.
Though Alan Turing is perhaps best known for his role in deciphering the Enigma code during World War II, he also developed a theoretical framework on pattern formation. Turing introduced the idea of reaction-diffusion as the basis for pattern formation, predicting that spontaneous chemical patterns could emerge from just two elements: diffusion and chemical reactions.
His pioneering work laid the groundwork for a new type of mathematical inquiry that applies reaction-diffusion equations to understanding natural phenomena. These naturally occurring patterns, often referred to as Turing patterns, are thought to be responsible for a variety of forms in nature, ranging from leopard spots to sand patterns on beaches and the arrangement of seeds in sunflowers. Although yet to be confirmed experimentally, Turing’s theories are believed to influence many natural patterns and find applications in multiple scientific fields, including biology, robotics, and even astrophysics.
Dr. Hermes Gadêlha, who leads the Polymaths Lab, along with his doctoral student James Cass, conducted this research at the University of Bristol’s School of Engineering Mathematics and Technology. Dr. Gadêlha stated that while spontaneous flagellar and ciliary motion is widely observed in nature, much remains unknown about its underlying mechanisms.
“These are fundamental for the health and pathology, reproduction, and survival of virtually every aquatic microorganism on Earth,” Gadêlha noted.
Inspired by recent findings regarding low-viscosity fluids, the team employed mathematical models, simulations, and data analytics to demonstrate that flagellar waves can emerge spontaneously, independent of their fluid surroundings. This is mathematically equivalent to Turing’s reaction-diffusion equations initially proposed for chemical pattern formation.
In the realm of sperm motility, chemical reactions fuel the molecular motors that power flagellar movement, and the resulting undulatory motion spreads along the tail as waves. The astonishing similarity between visual and motion patterns indicates that only two basic elements are needed to generate complex motion.
Dr. Gadêlha further elucidated that their mathematical “recipe” is followed by two biologically distinct species—bull sperm and Chlamydomonas (a model green algae)—suggesting that similar mechanisms are at play in nature.
“Even without the influence of surrounding fluids, traveling waves can spontaneously emerge on the flagellum. This suggests that flagella possess a robust mechanism to enable motion in low-viscosity environments, which would otherwise inhibit aquatic species,” added Dr. Gadêlha.
He thanked other researchers for making their data publicly accessible, allowing for this mathematical investigation. The results may eventually contribute to a better understanding of fertility challenges linked to abnormal flagellar motion and other diseases related to ineffective cilia in humans.
These discoveries also hold potential for applications in robotic technology, artificial muscles, and smart materials, as the team has unveiled a straightforward mathematical formula for generating motion patterns.
Dr. Gadêlha is also affiliated with the SoftLab at the Bristol Robotics Laboratory, where he applies pattern formation mathematics to innovate next-generation soft robotics.
“Turing laid the foundation for chemical pattern formation in 1952,” Gadêlha said. “We demonstrate that the most fundamental unit of motion in cellular organisms, the flagellum, follows Turing’s model to generate patterns of motion. While this takes us a step closer to decoding spontaneous natural motion mathematically, more extensive research is still required as our reaction-diffusion model is far from capturing all complexities.”
The research was funded by the Engineering and Physical Sciences Research Council (EPSRC) and a DTP studentship awarded to James Cass for his PhD work.
Computational tasks for this study were performed using the resources of the Advanced Computing Research Centre at the University of Bristol.
Citation: “The reaction-diffusion basis of animated patterns in eukaryotic flagella” by James Cass and Dr. Hermes Bloomfield-Gadêlha, published in Nature Communications on 27 September 2023.
DOI: 10.1038/s41467-023-41405-4
Table of Contents
Frequently Asked Questions (FAQs) about Pattern Formation
What is the primary focus of this study?
The primary focus of this study is to establish a mathematical connection between Alan Turing’s theories on pattern formation and the dynamics of sperm tail movement.
Who conducted the research?
The research was conducted by Dr. Hermes Gadêlha and his doctoral student James Cass at the University of Bristol’s School of Engineering Mathematics and Technology.
Where was the research published?
The findings of the research were published in the scientific journal Nature Communications on September 27, 2023.
What significance does this research hold for understanding natural patterns?
The research enriches our comprehension of natural patterns by revealing that the same mathematical principles that govern natural phenomena like stripes and spots also control the dynamics of biological entities, such as sperm tails.
Are there any potential applications for this research?
Yes, the research suggests potential applications in both healthcare and robotics. It may contribute to understanding fertility challenges associated with abnormal flagellar motion and could also find application in the development of robotic technology, artificial muscles, and smart materials.
How did the researchers carry out the study?
The research team used mathematical modeling, simulations, and data analytics. They were inspired by recent findings regarding low-viscosity fluids and showed that flagellar undulations can occur spontaneously, without being influenced by their fluid environment.
What is Turing’s reaction-diffusion theory?
Alan Turing’s reaction-diffusion theory posits that spontaneous patterns can emerge from just two elements: diffusion and chemical reactions. This theory is applied to understand various natural patterns and phenomena.
Is the study supported by experimental evidence?
While the study is highly suggestive, it acknowledges that more extensive research is needed to fully capture all complexities involved. It is a step closer to mathematically decoding natural patterns and phenomena but is not definitive.
Who funded the research?
The research was funded by the Engineering and Physical Sciences Research Council (EPSRC) and a DTP studentship awarded to James Cass for his PhD work.
What computational resources were used in this research?
The numerical work for this study was executed using the computational and data storage facilities of the Advanced Computing Research Centre at the University of Bristol.
More about Pattern Formation
- Nature Communications Journal
- Alan Turing’s Pattern Formation Theory
- University of Bristol School of Engineering
- Engineering and Physical Sciences Research Council (EPSRC)
- Advanced Computing Research Centre at the University of Bristol
- DOI for the Published Paper
- Overview of Reaction-Diffusion Systems
- Dr. Hermes Gadêlha’s Polymaths Lab
- SoftLab at Bristol Robotics Laboratory (BRL)
- Introduction to Ciliopathies


6 comments
Mathematical models decoding nature? As a techie, I find this utterly fascinating. cant wait to see how this research impacts future tech and medicine.
Seriously impressive research. I mean, linking math and natural patterns is one thing but extending it to healthcare and robotics? Thats next level.
Wow, this is some groundbreaking stuff right here. Turing keeps proving he was ahead of his time. Who would’ve thought his theories could be linked to something as biological as sperm movement?
i gotta say, the fact that this theory can be applied to different fields like biology and robotics is mind blowing. Turing was a real genius, man.
So this could even have implications for fertility treatments and stuff? That’s awesome. Science is so darn cool.
This isn’t just academic jargon, folks. This has real world applications that could change lives. Kudos to the research team. They’re onto something big.