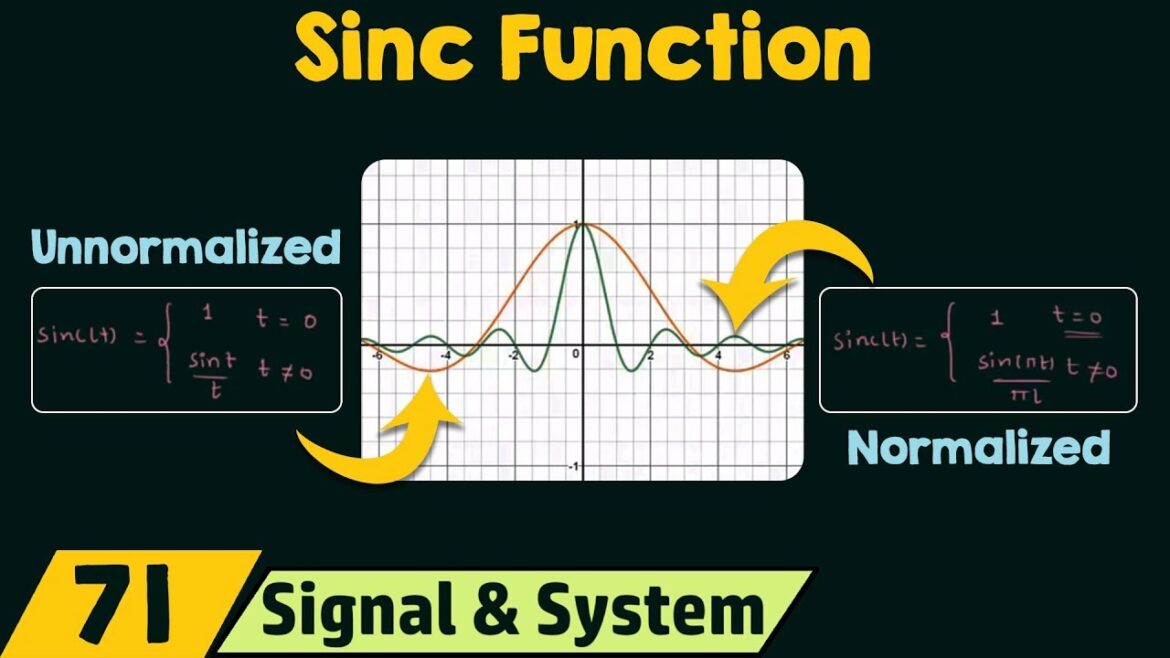
Sinc or sine cardinal is a function of mathematics. It is defined as the ratio of the length of the side opposite to the angle in a right angled triangle to the length of the hypotenuse. The sinc function is used extensively in signal processing and has important applications in engineering, physics, and computer science.
The name “sinc” is derived from its infinite series expansion, which is similar to that of the cosine function:
sin(x)/x=∑n=0∞((-1)^n/(2n+1))*x^(2n+1)
The sinc function can be extended to complex arguments z = x + iy using Euler’s formula:
sinc(z)=sin(πz)/(πz)=∑n=-∞∞((-1)^n/(2n+1))*e^(i(2n+1)z)
This extension allows for a wide range of applications in signal processing, such as interpolation, deconvolution, and image reconstruction. The sinc function also appears in many other areas of mathematics, such as Fourier analysis and number theory.